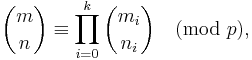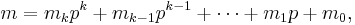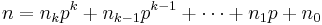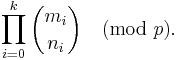Lucas' theorem
In number theory, the Lucas' theorem expresses the remainder of division of the binomial coefficient 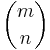 by a prime number p in terms of the base p expansions of the integers m and n.
by a prime number p in terms of the base p expansions of the integers m and n.
Lucas' theorem first appeared in 1878 in papers by Édouard Lucas.[1]
Contents |
Formulation
For non-negative integers m and n and a prime p, the following congruence relation holds:
where
and
are the base p expansions of m and n respectively.
Consequence
- A binomial coefficient
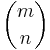 is divisible by a prime p if and only if at least one of the base p digits of n is greater than the corresponding digit of m.
is divisible by a prime p if and only if at least one of the base p digits of n is greater than the corresponding digit of m.
Proof
There are several ways to prove Lucas' theorem; here is a combinatorial argument. Let M be a set with m elements, and divide it into mi cycles of length pi for the various values of i. Then each of these cycles can be rotated separately, so that a group G which is the Cartesian product of cyclic groups Cpi acts on M. It thus also acts on subsets N of size n. Since the number of elements in G is a power of p, the same is true of any of its orbits. Thus in order to compute 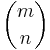 modulo p, we only need to consider fixed points of this group action. The fixed points are those subsets N that are a union of some of the cycles. More precisely one can show by induction on k-i, that N must have exactly ni cycles of size pi. Thus the number of choices for N is exactly
modulo p, we only need to consider fixed points of this group action. The fixed points are those subsets N that are a union of some of the cycles. More precisely one can show by induction on k-i, that N must have exactly ni cycles of size pi. Thus the number of choices for N is exactly
Variations and generalizations
- The valuation of the binomial coefficient
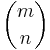 w.r.t. a prime p equals the number of carries that occur in addition of n and (m-n) in the base p.
w.r.t. a prime p equals the number of carries that occur in addition of n and (m-n) in the base p. - There exists a generalization of Lucas' theorem to the case of p being a power of prime.[2]
References
- ^
- Edouard Lucas (1878). "Théorie des Fonctions Numériques Simplement Périodiques". American Journal of Mathematics 1 (2): 184–196. doi:10.2307/2369308. JSTOR 2369308. MR1505161. (part 1);
- Edouard Lucas (1878). "Théorie des Fonctions Numériques Simplement Périodiques". American Journal of Mathematics 1 (3): 197–240. doi:10.2307/2369311. JSTOR 2369311. MR1505164. (part 2);
- Edouard Lucas (1878). "Théorie des Fonctions Numériques Simplement Périodiques". American Journal of Mathematics 1 (4): 289–321. doi:10.2307/2369373. JSTOR 2369373. MR1505176. (part 3)
- ^ Andrew Granville (1997). "Arithmetic Properties of Binomial Coefficients I: Binomial coefficients modulo prime powers". Canadian Mathematical Society Conference Proceedings 20: 253–275. MR1483922. http://www.dms.umontreal.ca/%7Eandrew/PDF/BinCoeff.pdf.